Расчёт рамы.

Строго говоря, рама автомобиля представляет собой сложную систему, так как часть нагрузки приложена не в продольных плоскостях, проходящих через точки опор. Однако, учитывая относительно небольшие нагрузки и расстояния между точками приложения сил и опорой, раму рассчитывают как обычную двухопорную балку.

В принятой схеме расчёта, нагрузки считают действующими в вертикальной плоскости. В систему сил включаются:

1. вес двигателя;
2. топливного бака с топливом;
3. груза в багажнике;
4. пяти пассажиров (если автомобиль двухместный то двух);
5. распределённая нагрузка от веса кузова.

Опорами являются места установки колёс.

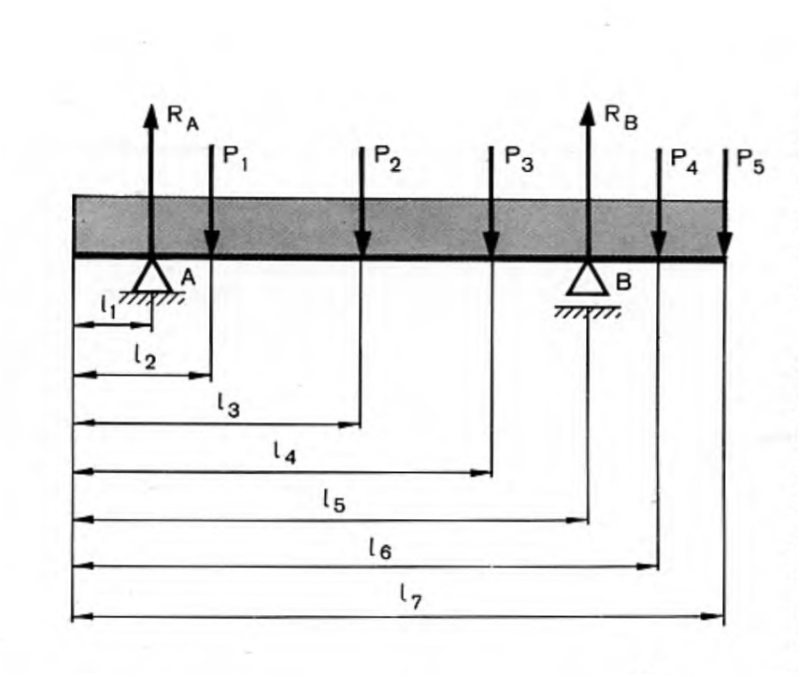
Обозначив действующие нагрузки через Р₁, Р₂, Р₃, Р₄, Р₅ (рис), распределённую нагрузку — через ql, расстояния до точек приложения нагрузок через l₁, l₂, l₃…,l₇, из условия равенства нулю моментов внешних сил определяют реакции в опорах R_A и R_B.

Для условия ?M_A= 0 (где M_A – момент сил относительно точки А)

0,5ql₁² – P₁ (l₂ – l₁) – P₂ (l₃ – l₁) – P₃ (l₄ – l₁) + R_B (l₅ – l₁) – P₄ (l₆ – l₁) – P₅ (l₇ – l₁) – 0,5q (l₇ – l₁)² = 0

Для условия ?M_B= 0 (где M_B – момент сил относительно точки B)

0,5ql₅² – R_A (l₅ – l₁) + P₁ (l₅ – l₂) + P₂ (l₅ – l₃) + P₃ (l₅ – l₄) – P₄ (l₆ – l₅) – P₅ (l₇ – l₅) – 0,5q (l₇ – l₅)² = 0

После определения реакций R_A и R_B в опорах проверяют выполнение условия равенства нулю суммы всех действующих сил в проекции на ось ординат

?Y= P₁ + P₂ + P₃ + P₄ + P₅ + ql₇ – R_A – R_B= 0

Затем рассчитывают изгибающие моменты в сечениях:

1. для первого сечения M₁ = -0,5ql₁²;
2. для второго сечения M₂ = -0,5ql₂² + R_A (l₂ – l₁);
3. для третьего сечения M₃ = -0,5ql₃² + R_A (l₃ – l₁) – P₁ (l₃ – l₂);
4. для четвёртого сечения M₄ = -0,5ql₄² + R_A (l₄ – l₁) – P₁ (l₄ – l₂) – P₂ (l₄ – l₃);
5. для пятого сечения M₅ = -0,5ql₅² + R_A (l₅ – l₁) P₁ (l₅ – l₂) – P₂ (l₅ – l₃) – P₃ (l₅ – l₄);
6. для шестого сечения M₆ = -0,5q (l₇ – L₀)² – P₅ (l₇ – l₆);
7. для седьмого сечения M₇ = 0.

где силы – в Н, длинна отрезков – в см.

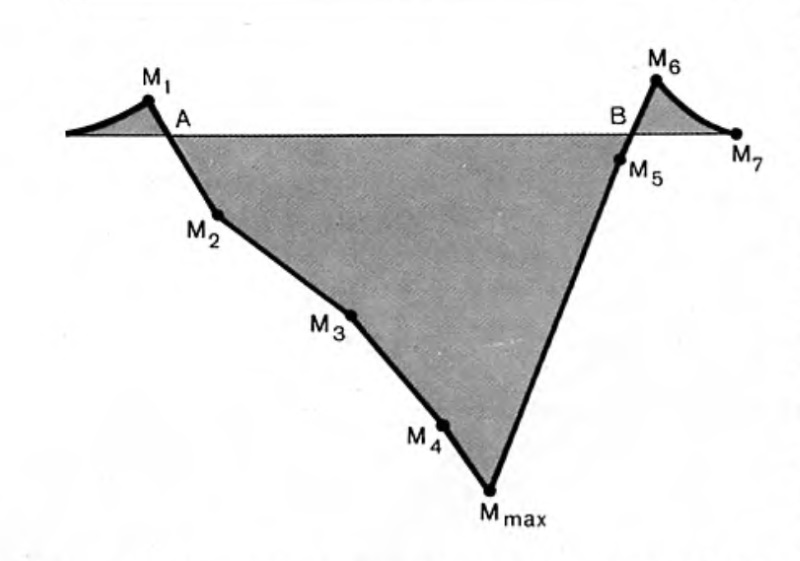
По вычисленным значениям изгибающих моментов строят эпюру.

Затем проводят анализ этой эпюры для определения максимального изгибающего момента M_MAX, для чего вводят текущую координату Х, считая, что в начале рамы Х = 0.

Определив максимальный изгибающий момент и задаваясь допускаемым напряжением (в Па), определяют необходимый момент сопротивления профиля лонжеронов с учетом того, что в работе участвуют два лонжерона и допущения, что на каждый из них действует одинаковая нагрузка:

W_X—X = M_MAX/[?],

где W_X—X – момент сопротивления профиля лонжерона, [?] – допускаемое напряжение при растяжении, Па.

По справочным данным выбирают необходимое сечение. В случаях, когда используется уже имеющийся профиль, проверяют его на прочность из условия, что:

? = M_MAX/W_X—X ?[?].

Если напряжение в точке максимального изгибающего момента превышает допустимое значение, то обычно усиливают лонжероны, применяя накладки, и повторно рассчитывают момент сопротивления этого соединения.

При самостоятельном изготовлении автомобиля обычно применяют еще и каркас для крепления кузова, который также воспринимает нагрузки. В связи с тем, что каркас повышает прочность кузова, его в расчёте не учитывают.

Приведённый расчёт рамы является приблизительным. С учётом коэффициента понижения допускаемых напряжений, равно 1,5. Можно использовать его с уверенностью, что рама будет надёжной в эксплуатации.

Данная статья была подготовлена по материалам книги «Я строю автомобиль» В. Захарченко и И. Туревский изд. «Машиностроение» 1989 г.